Planes in 3D space

A plane in 3D space can be thought of as a flat surface that stretches infinitely far, splitting space into two halves.

Planes have loads of uses in applications that deal with 3D geometry. I've mostly been working with them in the context of an architectural modeler, where geometry is defined in terms of planes and their intersections.

Learning about planes felt abstract and non-intuitive to me. “Sure, that's a plane equation, but what do I do with it? What does a plane look like?” It took some time for me to build an intuition for how to reason about and work with them.

In writing this, I want to provide you with an introduction that focuses on building a practical, intuitive understanding of planes. I hope to achieve this through the use of visual (and interactive!) explanations which will accompany us as we work through progressively more complex problems.

With that out of the way, let's get to it!

Describing planes

There are many ways to describe planes, such as through

1. a point in 3D space and a normal,
2. three points in 3D space, forming a triangle, or
3. a normal and a distance from an origin.

Starting with the point-and-normal case, here's an example of a plane described by a point in 3D space and a normal :

The normal describes the plane's orientation, where the surface of the plane is perpendicular to , while the point describes a point on the plane.

We described this plane in terms of a single point , but keep in mind that this plane—let's call it —contains infinitely many points.

If were described by one of those other points contained by , we would be describing the exact same plane. This is a result of the infinite nature of planes.

This way of describing planes—in terms of a point and a normal—is the point-normal form of planes.

We can also describe a plane using three points in 3D space , , forming a triangle:

The triangle forms an implicit plane, but for us to be able to do anything useful with the plane we'll need to calculate its normal . Once we've calculated the plane's normal, we can use that normal along with one of the triangle's three points to describe the plane in point-normal form.

As mentioned earlier, the normal describing a plane is a unit vector () perpendicular to the plane.

We can use and as two edge vectors that are parallel to the plane's surface.

By virtue of being parallel to the plane's surface, the vectors and are perpendicular to the plane's normal. This is where the cross product becomes useful to us.

The cross product takes in two vectors and and returns a vector that is perpendicular to both of them.

For example, given the vectors and , their cross product is the vector , which we'll label :

This explanation is simple on purpose. We'll get into more detail about the cross product later on.

Because the edge vectors of the triangle, and , are both parallel to the triangle's surface, their cross product will be perpendicular to the triangle's surface. Let's name the cross product of our two edge vectors :

has been scaled down for illustrative purposes

points in the right direction, but it's not a normal. For to be a normal, its magnitude needs to equal 1. We can normalize by dividing it by its magnitude, the result of which we'll assign to :

This gives us a normal where :

Having found the triangle's normal we can use it and any of the points , , to describe the plane containing the three points in point-normal form.

It doesn't matter which of , , we use as the point in the point-normal form; we always get the same plane.

Constant-normal form

There's one more way to describe a plane that we'll look at, which is through a normal and a distance .

This is the constant-normal form of planes. It makes lots of calculations using planes much simpler.

In the constant-normal form, the distance denotes how close the plane gets to the origin. Thought of another way: multiplying the normal by yields the point on the plane that's closest to the origin.

This is a simplification. More formally, given a point on a plane whose normal is , we can describe all points on the plane in two forms: the point-normal form , and the constant-normal form where . See further reading.

In getting a feel for the difference between the point-normal and constant-normal forms, take this example which describes the same plane in both forms:

The green arrow represents from the constant-normal form, while the blue point and arrow represent the point and normal from the point-normal form.

Translating from the point-normal to the constant-normal form is very easy: the distance is the dot product of and .

If you're not familiar with the dot product, don't worry. We'll cover it later on.

The normal stays the same across both forms.

Distance from plane

Given an arbitrary point and a plane in constant-normal form, we may want to ask how far away the point is from the plane. In other words, what is the minimum distance needs to travel to lie on the plane?

We can frame this differently if we construct a plane containing that is parallel to , which we can do in point-normal form using as the point and 's normal as the normal:

With two parallel planes, we can frame the problem as finding the distance between the two planes. This becomes trivial using their constant-normal form since it allows us to take the difference between their distance components and .

So let's find 's distance using the equation we learned about:

With two distances and from the planes and the solution simply becomes:

So, to simplify, given a plane having a normal and distance , we can calculate a point 's distance from like so:

The distance may be positive or negative depending on which side of the plane the point is on.

Projecting a point onto a plane

A case where calculating a point's distance from a plane becomes useful is, for example, if you want to project a point onto a plane.

Given a point which we want to project onto plane whose normal is and distance is , we can do that fairly easily. First, let's define as the point's distance from the plane:

Multiplying the plane's normal by gives us a vector which when added to projects it onto the plane. Let's call the projected point :

The projection occurs along the plane's normal, which is sometimes useful. However, it is much more useful to be able to project a point onto a plane along an arbitrary direction instead. Doing that boils down finding the point of intersection of a line and a plane.

Line-plane intersection

We can describe lines in 3D space using a point and normal . The normal describes the line's orientation, while the point describes a point which the line passes through.

In this chapter, the line will be composed of the point and normal , while the plane—given in constant-normal form—has a normal and a distance .

Our goal will be to find a distance that needs to travel along such that it lies on the plane.

We can figure out the distance that we'd need to travel if and were parallel, which is what we did when projecting along the plane's normal.

Let's try projecting along using as a scalar like so:

We'll visualize as a red point:

As and become parallel, gets us closer and closer to the correct solution. However, as the angle between and increases, becomes increasingly too small.

Here, the dot product comes in handy. For two vectors and , the dot product is defined as

where is the angle between and .

Consider the dot product of and . Since both normals are unit vectors whose magnitudes are 1

we can remove their magnitudes from the equation,

making the dot product of and the cosine of the angle between them.

For two vectors, the cosine of their angles approaches 1 as the vectors become increasingly parallel, and approaches 0 as they become perpendicular.

Since becomes increasingly too small as and become more perpendicular, we can use as a denominator for . We'll assign this scaled-up version of to :

With as our scaled-up distance, we find the point of intersection via:

We can now get rid of , which was defined as , giving us the full equation for :

Putting this into code, we get:

Vector3 LinePlaneIntersection(Line line, Plane plane) {
  float denom = Vector3.Dot(line.normal, plane.normal);
  float dist = Vector3.Dot(plane.normal, line.point);
  float D = (plane.distance - dist) / denom;
  return line.point + line.normal * D;
}

However, our code is not complete yet. In the case where the line is parallel to the plane's surface, the line and plane do not intersect.

That happens when and are perpendicular, in which case their dot product is zero. So if , the line and plane do not intersect. This gives us an easy test we can add to our code to yield a result of "no intersection".

However, for many applications we'll want to treat being almost parallel as actually being parallel. To do that, we can check whether the dot product is smaller than some very small number—customarily called epsilon

float denom = Vector3.Dot(line.normal, plane.normal);
if (Mathf.Abs(denom) < EPSILON) {
    return null; // Line is parallel to plane's surface
}

See if you can figure out why Mathf.Abs is used here. We'll cover it later, so you'll see if you're right.

We'll take a look at how to select the value of epsilon in a later chapter on two plane intersections.

With this, our line-plane intersection implementation becomes:

Vector3 LinePlaneIntersection(Line line, Plane plane) {
  float denom = Vector3.Dot(line.normal, plane.normal);
  if (Mathf.Abs(denom) < EPSILON) {
      return null; // Line is parallel to plane's surface
  }

  float dist = Vector3.Dot(plane.normal, line.point);
  float D = (plane.distance - dist) / denom;
  return line.point + line.normal * D;
}

Rays and lines

We've been talking about line-plane intersections, but I've been lying a bit by visualizing ray-plane intersections instead for visual clarity.

A ray and a line are very similar; they're both represented through a normal and a point .

The difference is that a ray (colored red) extends in the direction of away from , while a line (colored green) extends in the other direction as well:

What this means for intersections is that a ray will not intersect planes when traveling backward along its normal:

Our implementation for ray-plane intersections will differ from our existing line-plane intersection implementation only in that it should yield a result of "no intersection" when the ray's normal is pointing "away" from the plane's normal at an obtuse angle.

Since represents how far to travel along the normal to reach the point of intersection, we could yield "no intersection" when becomes negative:

if (D < 0) {
  return null;
}

But then we'd have to calculate first. That's not necessary since becomes negative as a consequence of the dot product being a negative number when and are at an obtuse angle between 90° and 180°.

If this feels non-obvious, it helps to remember that the dot product encodes the cosine of the angle between its two component vectors, which is why the dot product becomes negative for obtuse angles.

Knowing that, we can change our initial "parallel normals" test from this:

Vector3 LinePlaneIntersection(Line line, Plane plane) {
  float denom = Vector3.Dot(line.normal, plane.normal);
  if (Mathf.Abs(denom) < EPSILON) {
    return null; // Line is parallel to plane's surface
  }
  // ...
}

To this:

Vector3 RayPlaneIntersection(Line line, Plane plane) {
  float denom = Vector3.Dot(line.normal, plane.normal);
  if (denom < EPSILON) {
    // Ray is parallel to plane's surface or pointing away from it
    return null;
  }
  // ...
}

The check covers both the "line parallel to plane" case and the case where the two normal vectors are at an obtuse angle.

Note: is the symbol for epsilon.

Plane-plane intersection

The intersection of two planes forms an infinite line.

As a quick refresher: lines in 3D space are represented using a point and normal where normal describes the line's orientation, while the point describes a point which the line passes through.

Let's take two planes and whose normals are and .

Finding the direction vector of and 's intersection is deceptively simple. Since the line intersection of two planes lies on the surface of both planes, the line must be perpendicular to both plane normals, which means that the direction of the intersection is the cross product of the two plane normals. We'll assign it to .

The magnitude of the cross product is equal to the area of the parallelogram formed by the two component vectors. This means that we can't expect the cross product to be a unit vector, so we'll normalize and assign the normalized direction vector to .

This gives us the intersection's normal . Let's zoom in and see this close up.

But this is only half of the puzzle! We'll also need to find a point in space to represent the line of intersection (i.e. a point which the line passes through). We'll take a look at how to do just that, right after we discuss the no-intersection case.

Handling parallel planes

Two planes whose normals are parallel will never intersect, which is a case that we'll have to handle.

The cross product of two parallel normals is . So if , the planes do not intersect.

As previously mentioned, for many applications we'll want to treat planes that are almost parallel as being parallel. This means that our plane-plane intersection procedure should yield a result of "no intersection" when the magnitude of is less than some very small number called epsilon.

Line PlanePlaneIntersection(Plane P1, Plane P2) {
  Vector3 direction = Vector3.cross(P1.normal, P2.normal);
  if (direction.magnitude < EPSILON) {
    return null; // Roughly parallel planes
  }
  // ...
}

But what should the value of epsilon be?

Given two normals and where the angle between and is , we can find a reasonable epsilon by charting for different values of :

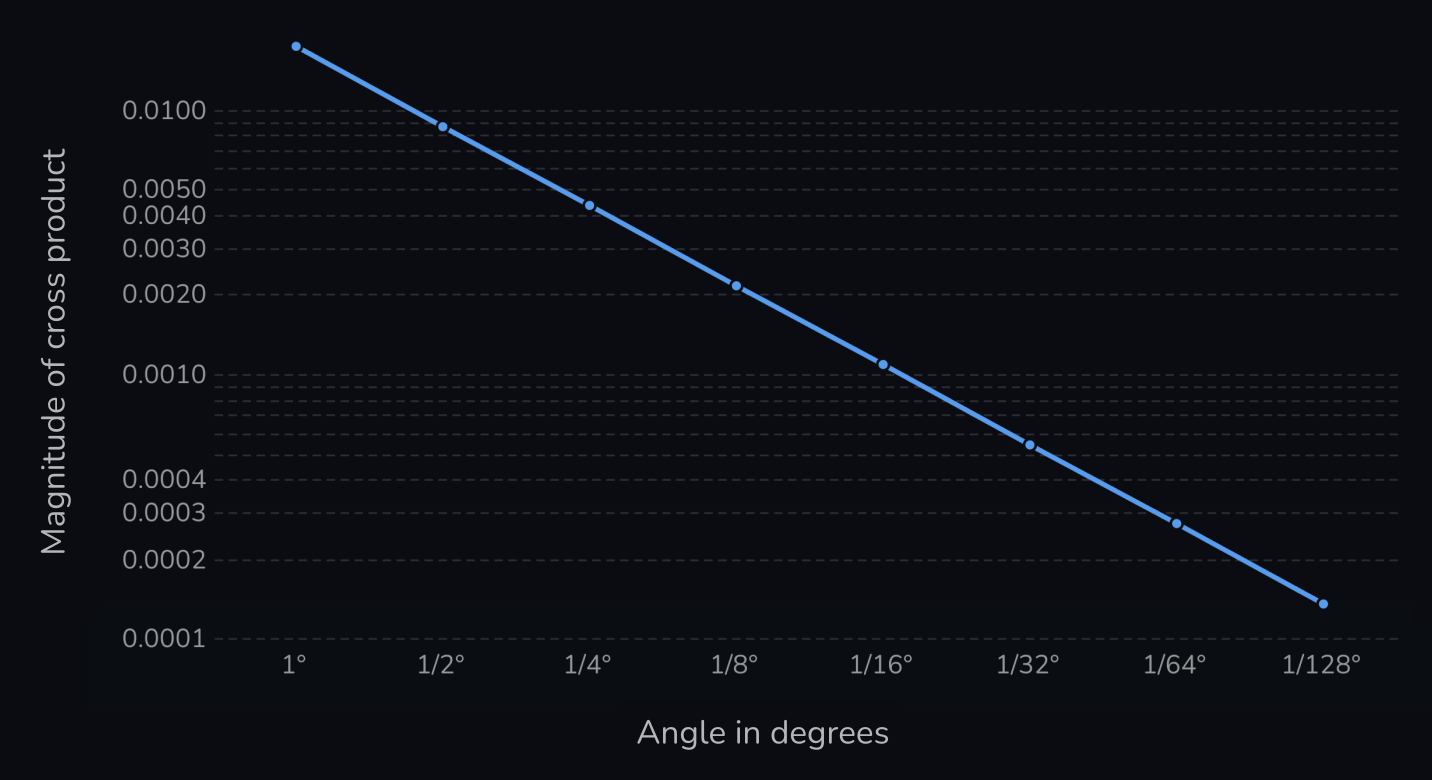
Both of the axes are logarithmic.

The relationship is linear: as the angle between the planes halves, so does the magnitude of the cross product of their normals. yields a magnitude of , and yields half of that.

So to determine the epsilon, we can ask: how low does the angle in degrees need to become for us to consider two planes parallel? Given an angle , we can find the epsilon via:

If that angle is 1/256°, then we get:

With this you can determine the appropriate epsilon based on how small the angle between the planes needs to be for you to consider them parallel. That will depend on your use case.

Finding a point of intersection

Having computed the normal and handled parallel planes, we can move on to finding a point along the line of intersection.

Since the line describing a plane-plane intersection is infinite, there are infinitely many points we could choose as .

We can narrow the problem down by taking the plane parallel to the two plane normals , and observing that it intersects the line at a single point.

Since the point lies on the plane parallel to the two plane normals, we can find it by exclusively traveling along those normals.

The simplest case is the one where and are perpendicular. In that case, the solution is just . Here's what that looks like visually:

When dragging the slider, notice how the tip of the parallelogram gets further away from the point of intersection as the planes become more parallel.

We can also observe that as we get further away from the point of intersection, the longer of the two vectors (colored red) pushes us further away from the point of intersection than the shorter (blue) vector does. This is easier to observe if we draw a line from the origin to the point of intersection:

Let's define and as the scaling factors that we apply to and (the result of which are the red and blue vectors). Right now we're using the distance components and of the planes as the scaling factors:

To solve this asymmetric pushing effect, we need to travel less in the direction of the longer vector as the planes become more parallel. We need some sort of "pulling factor" that adjusts the vectors such that their tip stays on the line as the planes become parallel.

Here our friend the dot product comes in handy yet again. When the planes are perpendicular the dot product of and equals 0, but as the planes become increasingly parallel, it approaches 1. We can use this to gradually increase our yet-to-be-defined pulling factor.

Let's give the dot product the name to make this a bit less noisy:

The perfect pulling factors happen to be the distance components and used as counterweights against each other!

Consider why this might be. When and are perpendicular, their dot product equals 0, which results in

which we know yields the correct solution.

In the case where and are parallel, their dot product equals 1, which results in:

Because the absolute values of and are equal, it means that the magnitude of the two vectors—defined as and —is equal:

This means that the magnitude of our vectors will become more equal as the planes become parallel, which is what we want!

Let's see this in action:

The vectors stay on the line, but they become increasingly too short as and become parallel.

Yet again, we can use the dot product. Since we want the length of the vectors to increase as the planes become parallel, we can divide our scalars and by where is the dot product of and and is the absolute value of .

The result of this looks like so:

Using as the denominator certainly increases the size of the parallelogram, but by too much.

However, notice what happens when we visualize the quadrants of the parallelogram:

As the planes become more parallel, the point of intersection approaches the center of the parallelogram.

In understanding why that is, consider the effect that our denominator has on the area of the parallelogram. When , both of the vectors forming the parallelogram double in length, which has the effect of quadrupling the area of the parallelogram.

This means that when we scale the component vectors of the parallelogram by

it has the effect of scaling the area of the parallelogram by:

To instead scale the area of the parallelogram by , we need to square in the denominator:

Squaring allows us to remove because the square of a negative number is positive.

With this, our scalars and become

which scales the parallelogram such that its tip lies at the point of intersection:

Putting all of this into code, we get:

float dot = Vector3.Dot(P1.normal, P2.normal);
float denom = 1 - dot * dot;

float k1 = (P1.distance - P2.distance * dot) / denom;
float k2 = (P2.distance - P1.distance * dot) / denom;

Vector3 point = P1.normal * k1 + P2.normal * k2;

Based on code from Real-Time Collision Detection by Christer Ericson

Which through some mathematical magic can be optimized down to:

Vector3 direction = Vector3.cross(P1.normal, P2.normal);

float denom = Vector3.Dot(direction, direction);
Vector3 a = P1.distance * P2.normal;
Vector3 b = P2.distance * P1.normal;
Vector3 point = Vector3.Cross(a - b, direction) / denom;

How this optimization works can be found in chapter 5.4.4 of Real-Time Collision Detection by Christer Ericson.

This completes our plane-plane intersection implementation:

Line PlanePlaneIntersection(Plane P1, Plane P2) {
  Vector3 direction = Vector3.cross(P1.normal, P2.normal);
  if (direction.magnitude < EPSILON) {
    return null; // Roughly parallel planes
  }

  float denom = Vector3.Dot(direction, direction);
  Vector3 a = P1.distance * P2.normal;
  Vector3 b = P2.distance * P1.normal;
  Vector3 point = Vector3.Cross(a - b, direction) / denom;

  Vector3 normal = direction.normalized;

  return new Line(point, normal);
}

By the way, an interesting property of only traveling along the plane normals is that it yields the point on the line of intersection that is closest to the origin. Cool stuff!

Three plane intersection

Given three planes , , , there are five possible configurations in which they intersect or don't intersect:

1. All three planes are parallel, with none of them intersecting each other.
2. Two of the planes are parallel, and the third plane intersects the other two.
3. All three planes intersect along a single line.
4. The three planes intersect each other in pairs, forming three parallel lines of intersection.
5. All three planes intersect each other at a single point.

When finding the point of intersection, we'll first need to determine whether all three planes intersect at a single point—which for configurations 1 through 4, they don't.

Given , , as the plane normals for , , , we can determine whether the planes intersect at a single point with the formula:

When I first saw this, I found it hard to believe this would work for all cases. Still, it does! Let's take a deep dive to better understand what's happening.

Two or more planes are parallel

We'll start with the configurations where two or more planes are parallel:

If and are parallel then is a vector whose magnitude is zero.

And since the dot product is a multiple of the magnitudes of its component vectors:

the final result is zero whenever and are parallel.

This takes care of the "all-planes-parallel" configuration, and the configuration where and are parallel

With that, let's consider the case where is parallel to either or but and are not parallel to each other.

Let's take the specific case where is parallel to but is parallel to neither.

Here the cross product is a vector (colored red) that's perpendicular to both and .

Since is parallel to , that means that is also perpendicular to . As we've learned, the dot product of two perpendicular vectors is zero, meaning that:

This also holds in the case where is parallel to instead of .

Parallel lines of intersection

We've demonstrated that two of the three normals being parallel results in . But what about the configurations where the three planes intersect along parallel lines? Those configurations have no parallel normals.

As we learned when looking at plane-plane intersections, the cross product of two plane normals gives us the direction vector of the planes' line of intersection.

When all of the lines of intersection are parallel, all of the plane normals defining those lines are perpendicular to them.

Yet again, because the dot product of perpendicular vectors is 0 we can conclude that for these configurations as well.

We can now begin our implementation. As usual, we'll use an epsilon to handle the "roughly parallel" case:

Vector3 ThreePlaneIntersection(Plane P1, Plane P2, Plane P3) {
  Vector3 cross = Vector3.Cross(P2.normal, P3.normal);
  float dot = Vector3.Dot(P1.normal, cross);
  if (Mathf.Abs(dot) < EPSILON) {
    return null; // Planes do not intersect at a single point
  }
  // ...
}

Computing the point intersection

We want to find the point at which our three planes , , intersect:

Some of what we learned about two-plane intersections will come into play here. Let's start by taking the line of intersection for and and varying the position of . You'll notice that the point of intersection is the point at which intersects the line.